You are currently browsing the tag archive for the ‘Complex Networks’ tag.
In order to solve hard combinatorial optimization problems (e.g. optimally scheduling students and teachers along a week plan on several different classes and classrooms), one way is to computationally mimic how ants forage the vicinity of their habitats searching for food. On a myriad of endless possibilities to find the optimal route (minimizing the travel distance), ants, collectively emerge the solution by using stigmergic signal traces, or pheromones, which also dynamically change under evaporation.
Current algorithms, however, make only use of a positive feedback type of pheromone along their search, that is, if they collectively visit a good low-distance route (a minimal pseudo-solution to the problem) they tend to reinforce that signal, for their colleagues. Nothing wrong with that, on the contrary, but no one knows however if a lower-distance alternative route is there also, just at the corner. On his global search endeavour, like a snowballing effect, positive feedbacks tend up to give credit to the exploitation of solutions but not on the – also useful – exploration side. The upcoming potential solutions can thus get crystallized, and freeze, while a small change on some parts of the whole route, could on the other-hand successfully increase the global result.
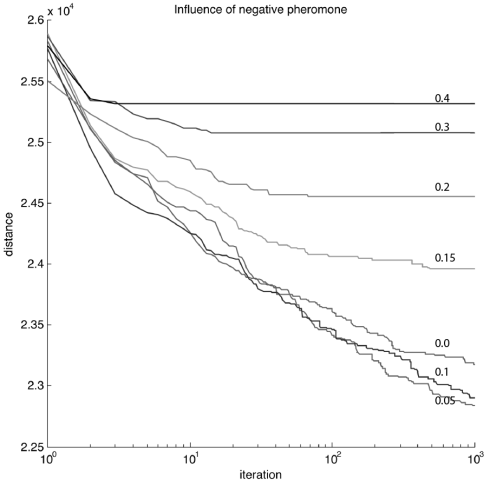Figure – Influence of negative pheromone on kroA100.tsp problem (fig.1 – page 6) (values on lines represent 1-ALPHA). A typical standard ACS (Ant Colony System) is represented here by the line with value 0.0, while better results could be found by our approach, when using positive feedbacks (0.95) along with negative feedbacks (0.05). Not only we obtain better results, as we found them earlier.
There is, however, an advantage when a second type of pheromone (a negative feedback one) co-evolves with the first type. And we decided to research for his impact. What we found out, is that by using a second type of global feedback, we can indeed increase a faster search while achieving better results. In a way, it’s like using two different types of evaporative traffic lights, in green and red, co-evolving together. And as a conclusion, we should indeed use a negative no-entry signal pheromone. In small amounts (0.05), but use it. Not only this prevents the whole system to freeze on some solutions, to soon, as it enhances a better compromise on the search space of potential routes. The pre-print article is available here at arXiv. Follows the abstract and keywords:
Vitorino Ramos, David M. S. Rodrigues, Jorge Louçã, “Second Order Swarm Intelligence” [PDF], in Hybrid Artificial Intelligent Systems, Lecture Notes in Computer Science, Springer-Verlag, Volume 8073, pp. 411-420, 2013.
Abstract: An artificial Ant Colony System (ACS) algorithm to solve general purpose combinatorial Optimization Problems (COP) that extends previous AC models [21] by the inclusion of a negative pheromone, is here described. Several Travelling Salesman Problem‘s (TSP) were used as benchmark. We show that by using two different sets of pheromones, a second-order co-evolved compromise between positive and negative feedbacks achieves better results than single positive feedback systems. The algorithm was tested against known NP complete combinatorial Optimization Problems, running on symmetrical TSPs. We show that the new algorithm compares favourably against these benchmarks, accordingly to recent biological findings by Robinson [26,27], and Grüter [28] where “No entry” signals and negative feedback allows a colony to quickly reallocate the majority of its foragers to superior food patches. This is the first time an extended ACS algorithm is implemented with these successful characteristics.
Keywords: Self-Organization, Stigmergy, Co-Evolution, Swarm Intelligence, Dynamic Optimization, Foraging, Cooperative Learning, Combinatorial Optimization problems, Symmetrical Travelling Salesman Problems (TSP).
Figure – Hybrid Artificial Intelligent Systems new LNAI (Lecture Notes on Artificial Intelligence) series volume 8073, Springer-Verlag Book [original photo by my colleague David M.S. Rodrigues].
New work, new book. Last week one of our latest works come out published on Springer. Edited by Jeng-Shyang Pan, Marios M. Polycarpou, Emilio Corchado et al. “Hybrid Artificial Intelligent Systems” comprises a full set of new papers on this hybrid area on Intelligent Computing (check the full articles list at Springer). Our new paper “Second Order Swarm Intelligence” (pp. 411-420, Springer books link) was published on the Bio-inspired Models and Evolutionary Computation section.
Recent research have increasingly being focused on the relationship between Human-Human interaction, social networks (no, not the Facebook) and other Human-activity areas, like health. Nicholas Christakis (Harvard Univ. research link) points us that, people are inter-connected, and so as well, their health is inter-connected. This research engages two types of phenomena: the social, mathematical, and biological rules governing how social networks form (“Connection“) and the biological and social implications of how they operate to influence thoughts, feelings, and behaviours (“Contagion“), as in the self-organized stigmergy-like dynamics of Cognitive Collective Perception (link).
Above, Nicholas Christakis (in a 56m. documentary lecture produced by The Floating University, Sept. 2011) discusses the obvious tension and delicate balance between agency (one individual choices and actions) and structure (our collective responsibility), where here, structure refers not only to our co-evolving dynamic societal environment as well as to the permanent unfolding entangled nature of topological structure on complex networks, such as in human-human social networks, while asking: If you’re so free, why do you follow others? The documentary (YouTube link) resume states:
“If you think you’re in complete control of your destiny or even your own actions, you’re wrong. Every choice you make, every behaviour you exhibit, and even every desire you have finds its roots in the social universe. Nicholas Christakis explains why individual actions are inextricably linked to sociological pressures; whether you’re absorbing altruism performed by someone you’ll never meet or deciding to jump off the Golden Gate Bridge, collective phenomena affect every aspect of your life. By the end of the lecture Christakis has revealed a startling new way to understand the world that ranks sociology as one of the most vitally important social sciences.”
While cooperation is central to the success of human societies and is widespread, cooperation in itself, however, poses a challenge in both the social and biological sciences: How can this high level of cooperation be maintained in the face of possible exploitation? One answer involves networked interactions and population structure.
As perceived, the balance between homophily (where “birds of a feather flock together”) and heterophily (one where most of genotypes are negatively correlated), do requires further research. In fact, in humans, one of the most replicated findings in the social sciences is that people tend to associate with other people that they resemble, a process precisely known as homophily. As Christakis points out, although phenotypic resemblance between friends might partly reflect the operation of social influence, our genotypes are not materially susceptible to change. Therefore, genotypic resemblance could result only from a process of selection. Such genotypic selection might in turn take several forms. For short, let me stress you two examples. What follows are two papers, as well as a quick reference (image below) to a recent general-audience of his books:
1) Rewiring your network fosters cooperation:
“Human populations are both highly cooperative and highly organized. Human interactions are not random but rather are structured in social networks. Importantly, ties in these networks often are dynamic, changing in response to the behavior of one’s social partners. This dynamic structure permits an important form of conditional action that has been explored theoretically but has received little empirical attention: People can respond to the cooperation and defection of those around them by making or breaking network links. Here, we present experimental evidence of the power of using strategic link formation and dissolution, and the network modification it entails, to stabilize cooperation in sizable groups. Our experiments explore large-scale cooperation, where subjects’ cooperative actions are equally beneficial to all those with whom they interact. Consistent with previous research, we find that cooperation decays over time when social networks are shuffled randomly every round or are fixed across all rounds. We also find that, when networks are dynamic but are updated only infrequently, cooperation again fails. However, when subjects can update their network connections frequently, we see a qualitatively different outcome: Cooperation is maintained at a high level through network rewiring. Subjects preferentially break links with defectors and form new links with cooperators, creating an incentive to cooperate and leading to substantial changes in network structure. Our experiments confirm the predictions of a set of evolutionary game theoretic models and demonstrate the important role that dynamic social networks can play in supporting large-scale human cooperation.”, abstract in D.G. Rand, S. Arbesman, and N.A. Christakis, “Dynamic Social Networks Promote Cooperation in Experiments with Humans,” PNAS: Proceedings of the National Academy of Sciences (October 2011). [full PDF];
Picture – (book cover) Along with James Fowler, Christakis has authored also a general-audience book on social networks: Connected: The Surprising Power of Our Social Networks and How They Shape Our Lives, 2011 (book link). For a recent book review, access here.
2) We are surrounded by a sea of our friends’ genes:
“It is well known that humans tend to associate with other humans who have similar characteristics, but it is unclear whether this tendency has consequences for the distribution of genotypes in a population. Although geneticists have shown that populations tend to stratify genetically, this process results from geographic sorting or assortative mating, and it is unknown whether genotypes may be correlated as a consequence of nonreproductive associations or other processes. Here, we study six available genotypes from the National Longitudinal Study of Adolescent Health to test for genetic similarity between friends. Maps of the friendship networks show clustering of genotypes and, after we apply strict controls for population strati!cation, the results show that one genotype is positively correlated (homophily) and one genotype is negatively correlated (heterophily). A replication study in an independent sample from the Framingham Heart Study veri!es that DRD2 exhibits signi!cant homophily and that CYP2A6 exhibits signi!cant heterophily. These unique results show that homophily and heterophily obtain on a genetic (indeed, an allelic) level, which has implications for the study of population genetics and social behavior. In particular, the results suggest that association tests should include friends’ genes and that theories of evolution should take into account the fact that humans might, in some sense, be metagenomic with respect to the humans around them.”, abstract in J.H. Fowler, J.E. Settle, and N.A. Christakis, “Correlated Genotypes in Friendship Networks,” PNAS: Proceedings of the National Academy of Sciences (January 2011). [full PDF].
Remove one network edge and see what happens. Then, two… etc. This is the first illustration on Mark Buchanan “Nexus: Small-worlds and the ground-breaking science of networks” 2002 book – Norton, New York (Prelude, page 17), representing a portion of the food web for the Benguela ecosystem, located off the western coast of South Africa (from Peter Yodzis). For a joint review of 3 general books in complex networks, including Barabási‘s “Linked“, Duncan Watts “Small-Worlds” and Buchanan‘s “Nexus” pay a visit into JASSS – Journal of Artificial Societies and Social Simulation, ‘a review of three books’ entry by Frédéric Amblard (link).
Video lecture – In this new RSA Animate, Manuel Lima, senior UX design lead at Microsoft Bing, explores the power of network visualisation to help navigate our complex modern world. Taken from a lecture given by Manuel Lima as part of the RSA’s free public events programme.
Network visualization has experienced a meteoric rise in the last decade, bringing together people from various fields and capturing the interest of individuals across the globe. As the practice continues to shed light on an incredible array of complex issues, it keeps drawing attention back onto itself. Manuel Lima is a Senior UX Design Lead at Microsoft Bing and founder of VisualComplexity.com, and was nominated as ‘one of the 50 most creative and influential minds of 2009’ by Creativity Magazine. He visits the RSA to explore a critical paradigm shift in various areas of knowledge, as we stop relying on hierarchical tree structures and turn instead to networks in order to properly map the inherent complexities of our modern world. The talk will showcase a variety of captivating examples of visualization and also introduce the network topology as a new cultural meme. (from RSA, lecture link).
Ever tried to solve a problem where its own problem statement is changing constantly? Have a look on our approach:
Vitorino Ramos, David M.S. Rodrigues, Jorge Louçã, “Spatio-Temporal Dynamics on Co-Evolved Stigmergy“, in European Conference on Complex Systems, ECCS’11, Vienna, Austria, Sept. 12-16 2011.
Abstract: Research over hard NP-complete Combinatorial Optimization Problems (COP’s) has been focused in recent years, on several robust bio-inspired meta-heuristics, like those involving Evolutionary Computation (EC) algorithmic paradigms. One particularly successful well-know meta-heuristic approach is based on Swarm Intelligence (SI), i.e., the self-organized stigmergic-based property of a complex system whereby the collective behaviors of (unsophisticated) entities interacting locally with their environment cause coherent functional global patterns to emerge. This line of research recognized as Ant Colony Optimization (ACO), uses a set of stochastic cooperating ant-like agents to find good solutions, using self-organized stigmergy as an indirect form of communication mediated by artificial pheromone, whereas agents deposit pheromone-signs on the edges of the problem-related graph complex network, encompassing a family of successful algorithmic variations such as: Ant Systems (AS), Ant Colony Systems (ACS), Max-Min Ant Systems (Max–Min AS) and Ant-Q.
Albeit being extremely successful these algorithms mostly rely on positive feedback’s, causing excessive algorithmic exploitation over the entire combinatorial search space. This is particularly evident over well known benchmarks as the symmetrical Traveling Salesman Problem (TSP). Being these systems comprised of a large number of frequently similar components or events, the principal challenge is to understand how the components interact to produce a complex pattern feasible solution (in our case study, an optimal robust solution for hard NP-complete dynamic TSP-like combinatorial problems). A suitable approach is to first understand the role of two basic modes of interaction among the components of Self-Organizing (SO) Swarm-Intelligent-like systems: positive and negative feedback. While positive feedback promotes a snowballing auto-catalytic effect (e.g. trail pheromone upgrading over the network; exploitation of the search space), taking an initial change in a system and reinforcing that change in the same direction as the initial deviation (self-enhancement and amplification) allowing the entire colony to exploit some past and present solutions (environmental dynamic memory), negative feedback such as pheromone evaporation ensure that the overall learning system does not stables or freezes itself on a particular configuration (innovation; search space exploration). Although this kind of (global) delayed negative feedback is important (evaporation), for the many reasons given above, there is however strong assumptions that other negative feedbacks are present in nature, which could also play a role over increased convergence, namely implicit-like negative feedbacks. As in the case for positive feedbacks, there is no reason not to explore increasingly distributed and adaptive algorithmic variations where negative feedback is also imposed implicitly (not only explicitly) over each network edge, while the entire colony seeks for better answers in due time.
In order to overcome this hard search space exploitation-exploration compromise, our present algorithmic approach follows the route of very recent biological findings showing that forager ants lay attractive trail pheromones to guide nest mates to food, but where, the effectiveness of foraging networks were improved if pheromones could also be used to repel foragers from unrewarding routes. Increasing empirical evidences for such a negative trail pheromone exists, deployed by Pharaoh’s ants (Monomorium pharaonis) as a ‘no entry‘ signal to mark unrewarding foraging paths. The new algorithm comprises a second order approach to Swarm Intelligence, as pheromone-based no entry-signals cues, were introduced, co-evolving with the standard pheromone distributions (collective cognitive maps) in the aforementioned known algorithms.
To exhaustively test his adaptive response and robustness, we have recurred to different dynamic optimization problems. Medium-size and large-sized dynamic TSP problems were created. Settings and parameters such as, environmental upgrade frequencies, landscape changing or network topological speed severity, and type of dynamic were tested. Results prove that the present co-evolved two-type pheromone swarm intelligence algorithm is able to quickly track increasing swift changes on the dynamic TSP complex network, compared to standard algorithms.
Keywords: Self-Organization, Stigmergy, Co-Evolution, Swarm Intelligence, Dynamic Optimization, Foraging, Cooperative Learning, Combinatorial Optimization problems, Dynamical Symmetrical Traveling Salesman Problems (TSP).
Fig. – Recovery times over several dynamical stress tests at the fl1577 TSP problem (1577 node graph) – 460 iter max – Swift changes at every 150 iterations (20% = 314 nodes, 40% = 630 nodes, 60% = 946 nodes, 80% = 1260 nodes, 100% = 1576 nodes). [click to enlarge]
David M.S. Rodrigues, Jorge Louçã, Vitorino Ramos, “From Standard to Second Order Swarm Intelligence Phase-space maps“, in European Conference on Complex Systems, ECCS’11, Vienna, Austria, Sept. 12-16 2011.
Abstract: Standard Stigmergic approaches to Swarm Intelligence encompasses the use of a set of stochastic cooperating ant-like agents to find optimal solutions, using self-organized Stigmergy as an indirect form of communication mediated by a singular artificial pheromone. Agents deposit pheromone-signs on the edges of the problem-related graph to give rise to a family of successful algorithmic approaches entitled Ant Systems (AS), Ant Colony Systems (ACS), among others. These mainly rely on positive feedback’s, to search for an optimal solution in a large combinatorial space. The present work shows how, using two different sets of pheromones, a second-order co-evolved compromise between positive and negative feedback’s achieves better results than single positive feedback systems. This follows the route of very recent biological findings showing that forager ants, while laying attractive trail pheromones to guide nest mates to food, also gained foraging effectiveness by the use of pheromones that repelled foragers from unrewarding routes. The algorithm presented here takes inspiration precisely from this biological observation.
The new algorithm was exhaustively tested on a series of well-known benchmarks over hard NP-complete Combinatorial Optimization Problems (COP’s), running on symmetrical Traveling Salesman Problems (TSP). Different network topologies and stress tests were conducted over low-size TSP’s (eil51.tsp; eil78.tsp; kroA100.tsp), medium-size (d198.tsp; lin318.tsp; pcb442.tsp; att532.tsp; rat783.tsp) as well as large sized ones (fl1577.tsp; d2103.tsp) [numbers here referring to the number of nodes in the network]. We show that the new co-evolved stigmergic algorithm compared favorably against the benchmark. The algorithm was able to equal or majorly improve every instance of those standard algorithms, not only in the realm of the Swarm Intelligent AS, ACS approach, as in other computational paradigms like Genetic Algorithms (GA), Evolutionary Programming (EP), as well as SOM (Self-Organizing Maps) and SA (Simulated Annealing). In order to deeply understand how a second co-evolved pheromone was useful to track the collective system into such results, a refined phase-space map was produced mapping the pheromones ratio between a pure Ant Colony System (where no negative feedback besides pheromone evaporation is present) and the present second-order approach. The evaporation rate between different pheromones was also studied and its influence in the outcomes of the algorithm is shown. A final discussion on the phase-map is included. This work has implications in the way large combinatorial problems are addressed as the double feedback mechanism shows improvements over the single-positive feedback mechanisms in terms of convergence speed and on major results.
Keywords: Stigmergy, Co-Evolution, Self-Organization, Swarm Intelligence, Foraging, Cooperative Learning, Combinatorial Optimization problems, Symmetrical Traveling Salesman Problems (TSP), phase-space.
Fig. – Comparing convergence results between Standard algorithms vs. Second Order Swarm Intelligence, over TSP fl1577 (click to enlarge).
Picture – The European Conference on Complex Systems (ECCS’11 – link) at one of the main Austrian newspapers Der Standard: “Die ganze Welt als Computersimulation” (link), Klaus Taschwer, Der Standard, 14 September [click to enlarge – photo taken at the conference on Sept. 15, Vienna 2011].
“Take Darwin, for example: would Caltech have hired Darwin? Probably not. He had only vague ideas about some of the mechanisms underlying biological Evolution. He had no way of knowing about genetics, and he lived before the discovery of mutations. Nevertheless, he did work out, from the top down, the notion of natural selection and the magnificent idea of the relationship of all living things.” Murray Gell-Mann in “Plectics“, excerpted from The Third Culture: Beyond the Scientific Revolution by John Brockman (Simon & Schuster, 1995).
To be honest, I didn’t enjoy this title, but all of us had a fair share with journalists, now and then by now. After all, 99% of us don’t do computer simulation. We are all after the main principles, and their direct applications.
During 5 days (12-16 Sept.), with around 700 attendees the Vienna 2011 conference evolved around main important themes as Complexity & Networks (XNet), Current Trends in Game Theory, Complexity in Energy Infrastructures, Emergent Properties in Natural and Artificial Complex Systems (EPNACS), Complexity and the Future of Transportation Systems, Econophysics, Cultural and Opinion Dynamics, Dynamics on and of Complex Networks, Frontiers in the Theory of Evolution, and – among many others – Dynamics of Human Interactions.
For those who know me (will definitely understand), I was mainly attending those sessions underlined above, the last one (Frontiers in Evolution) being one of my favorites, among all these ECCS years. All in all, the conference had highly quality works (daily, we had about 3-4 works I definitely think should be followed in the future) and to those, more attention should be deserved (my main critics to the conference organization goes in here). Naturally, the newspaper article also reflects on the FuturICT, being historically one of the major scientific European projects ever done (along, probably, with the Geneva LHC), which teams spread across Europe, including Portugal with a representative team of 7 members present on the conference, led by Jorge Louçã, the former editor and organizer on the previous ECCS’10 last year in Lisbon.
Video – “… they forgot to say: in principle!“. Ricard Solé addressing the topic of a Morphospace for Biological Computation at ECCS’11 (European Conference on Complex Systems), while keeping is good humor on.
Let me draw anyway your attention to 4 outstanding lectures: Peter Schuster (link) on the first day, dissected on the source of Complexity in Evolution, battling among – as he puts it – two paradoxes: (1) Evolution is an enormously complex process, and (2) biological evolution on Earth proceeds from lower towards higher complexity. Earlier on that morning – opening the conference -, Murray Gell-Mann (link) who co-founded the Santa Fe Institute in 1984, gave a wonderful lecture on Generalized Entropies. Besides his age, the 1969 Nobel Prize in physics for his work on the theory of elementary particles, gladly turned his interest in the 1990s to the theory of Complex Adaptive Systems (CAS). Next, Albert-László Barabási (link), tamed Complexity on Controlling Networks. Finally, at the last day, closing the conference in pure gold, Ricard Solé (link) addressed the topic of a Morphospace for Biological Computation, an amazing lecture with a powerful topic to which – nevertheless – I felt he had little time (20 minutes), for such a rich endeavor. However – by no means -, he have lost his good humor during the talk (check my video above). Next year, the conference will be held in Brussels, and by just judging at the poster design, it promises. Go ants, go … !
Picture – The European Conference on Complex Systems (ECCS’12 – link) poster design for next year in Brussels.
Fig. – A cartoon by Nitrozac and Snaggy (The Joy of Tech, link) July 2011 [Geek Culture]. Click to enlarge.
The importance of Network Topology again… at [PLoS]. Abstract: […] The performance of information processing systems, from artificial neural networks to natural neuronal ensembles, depends heavily on the underlying system architecture. In this study, we compare the performance of parallel and layered network architectures during sequential tasks that require both acquisition and retention of information, thereby identifying tradeoffs between learning and memory processes. During the task of supervised, sequential function approximation, networks produce and adapt representations of external information. Performance is evaluated by statistically analyzing the error in these representations while varying the initial network state, the structure of the external information, and the time given to learn the information. We link performance to complexity in network architecture by characterizing local error landscape curvature. We find that variations in error landscape structure give rise to tradeoffs in performance; these include the ability of the network to maximize accuracy versus minimize inaccuracy and produce specific versus generalizable representations of information. Parallel networks generate smooth error landscapes with deep, narrow minima, enabling them to find highly specific representations given sufficient time. While accurate, however, these representations are difficult to generalize. In contrast, layered networks generate rough error landscapes with a variety of local minima, allowing them to quickly find coarse representations. Although less accurate, these representations are easily adaptable. The presence of measurable performance tradeoffs in both layered and parallel networks has implications for understanding the behavior of a wide variety of natural and artificial learning systems. […] (*)
(*) in Hermundstad AM, Brown KS, Bassett DS, Carlson JM, 2011 Learning, Memory, and the Role of Neural Network Architecture. PLoS Comput Biol 7(6): e1002063. doi:10.1371/journal.pcbi.1002063
Drawing (page 5) – Riccardo Manzotti – A Process View of Reality – April 2008.
“To destroy variety at a scale, we need variety at another scale“, Yavni Bar-Yam, ICCS’11 – Int. Conference on Complex Systems, Boston, June 2011.
In “a process oriented externalist solution to the hard problem” (A Process View of Reality, 2008), an 8 page comic series (pdf link) about the Mind-Body problem, or David Chalmers Hard Problem, Riccardo Manzotti asks: […] How can the conscious mind emerge out of physical stuff like the brain? Apparently, Science faces an unsolvable problem: The hard problem states that there is an unbridgeable gap between our conscious experience and the scientific description of the world. The modern version of the mind-body problem arose when the scholars of the XVII century suggested that reality is divided in the mental domain and in the physical domain […]. In the next 7 pages, Manzotti comes up with a possible solution, not far from what Science nowadays is doing, starting in the 1950’s: avoiding reductionism.
Video – “Be the one” track on Moby‘s Destroyed album. Destroyed is the tenth studio album by the American electronic artist Moby. It was released on 2011 by Mute Records. Network video animation by Taras Gesh.
From time to time some colleagues, students and friends do ask me what is a good introductory paper into Complex Networks. Indeed there are several, including some general books, but over the years I tend to point into “The Shortest Path to Complex Networks” by J.F.F. Mendes (thorough my life I met him several times now) and S.N. Dorogovtsev, released in 2004. For those who are beginners on the field, and do want to play or indeed program several concepts in the area, like clustering, small-worlds, edge condensation, cliques and communities as well as the preferential attachment (point 20.) among others, this is a rather simple and quick (besides is 25 pages) straightforward paper, well organized around 51 different entries, topics and concepts. Not all of them are here of course, like, among others, the age node issue which for several reasons tends to interest me. Point 1 starts with the birth of network science and it’s simple as : […] In 1735, in St Petersburg, Leonhard Euler solved the so-called Konigsberg bridge problem – walks on a simple small graph. This solution (actually, a proof) is usually considered as a starting point of the science of networks […]. The full paper is available through arXiv.org. Here is the link. Do enjoy. Like Moby says… be the one. The full reference list is also a must.
Fig. – (today’s NATURE Journal cover, Vol. 473 N. 7346 May 12 2011) Control theory can be used to steer engineered and natural systems towards a desired state, but a framework to control complex self-organized systems is lacking. Can such networks be controlled? Albert-László Barabási and colleagues tackle this question and arrive at precise mathematical answers that amount to ‘yes, up to a point’. They develop analytical tools to study the controllability of an arbitrary complex directed network using both model and real systems, ranging from regulatory, neural and metabolic pathways in living organisms to food webs, cell-phone movements and social interactions. They identify the minimum set of driver nodes whose time-dependent control can guide the system’s entire dynamics. Surprisingly, these are not usually located at the network hubs. On the cover, part of the cactus structure, a subset of nodes that have a key role in the control of real networks, with nodes in blue and drivers in red, visualized by Mauro Martino.
What follows are excerpts from the Northeastern University press realise (here) deliver today:
(May 12, 2011) […] Northeastern University researchers are offering a fascinating glimpse into how greater control of complex systems, such as cellular networks and social media, can be achieved by merging the tools of network science and control theory. Albert-László Barabási and Yang-Yu Liu coauthored a paper on the research findings, featured as the cover story in the May 12 issue of the journal Nature. Barabási, a world-renowned network scientist, is a distinguished professor in the Departments of Physics and Biology and the College of Computer and Information Science, and is the founding director of Northeastern’s Center for Complex Network Research. Liu is a postdoctoral research associate in Barabasi’s lab.
The researchers said this approach can lead to major strides in understanding complex engineering and biological systems. For example, controlling the neural and metabolic pathways in living organisms could lead to health-care breakthroughs in drug discovery and disease treatments. “Most large complex networks have been created for some practical purpose: metabolic networks to process the food we eat, the Internet to transfer information, organizational networks to achieve the goals of an organization,” said Barabási. “The tools developed in this paper offer the possibility to better understand how to control these systems. This could potentially generate more efficient metabolic pathways, with applications in developing cures to metabolic diseases, to offering new insights into the design of better organizations.”
Barabási and Liu collaborated with MIT researcher Jean-Jacques Slotine on the paper. The researchers note that control theory already offers mathematical tools for steering engineered and natural systems — such as synchronized manufacturing processes, cars, robots and electrical circuits — toward a desired state. However, they said a framework is lacking to take charge of complex, self-organized systems — such as cellular and social networks. To meet this challenge, they combined the principles of control theory with their innovative network science research to develop an algorithm that can assess the driver nodes, or connection points, within a particular complex network. By doing so, they can determine how many nodes are necessary to control in order to gain control of the system.
The trio was interested in discovering the minimum number of driver nodes needed to control a complex network. They found that denser networks with more connections — such as online social networks — were easier to control than cellular networks. They also found that sparse networks, like many biological and communication networks, are the hardest to control. Liu said this work represents a fundamental contribution to both control theory and network science research. “This work was not possible 10 years ago, because at that time we didn’t know how to categorize these complex networks. We didn’t have the data,” Liu said. “But today, we have the data available for empirical studies on many large-scale networks.” […]
Figure – Understanding the Brain as a Computational Network: significant neuronal motifs of size 3. Most over-represented colored motifs of size 3 in the C. elegans complex neuronal network. Green: sensory neuron; blue: motor neuron; red: interneuron. Arrows represent direction that the signal travels between the two cells. (from Adami et al. 2011 [Ref. below])
Abstract: […] Complex networks can often be decomposed into less complex sub-networks whose structures can give hints about the functional organization of the network as a whole. However, these structural motifs can only tell one part of the functional story because in this analysis each node and edge is treated on an equal footing. In real networks, two motifs that are topologically identical but whose nodes perform very different functions will play very different roles in the network. Here, we combine structural information derived from the topology of the neuronal network of the nematode C. elegans with information about the biological function of these nodes, thus coloring nodes by function. We discover that particular colorations of motifs are significantly more abundant in the worm brain than expected by chance, and have particular computational functions that emphasize the feed-forward structure of information processing in the network, while evading feedback loops. Interneurons are strongly over-represented among the common motifs, supporting the notion that these motifs process and transduce the information from the sensor neurons towards the muscles. Some of the most common motifs identified in the search for significant colored motifs play a crucial role in the system of neurons controlling the worm’s locomotion. The analysis of complex networks in terms of colored motifs combines two independent data sets to generate insight about these networks that cannot be obtained with either data set alone. The method is general and should allow a decomposition of any complex networks into its functional (rather than topological) motifs as long as both wiring and functional information is available. […] from Qian J, Hintze A, Adami C (2011) Colored Motifs Reveal Computational Building Blocks in the C. elegans Brain, PLoS ONE 6(3): e17013. doi:10.1371/journal.pone.0017013
[…] The role of evolution in producing these patterns is clear, said Adami. “Selection favors those motifs that impart high fitness to the organism, and suppresses those that work against the task at hand.” In this way, the efficient and highly functional motifs (such as the sensory neuron-interneuron-motor neuron motif) are very common in the nervous system, while those that would waste energy and give no benefit to, or even harm, the animal are not found in the network. “Adami and his team have used evolutionary computation to develop hypotheses about the evolution of neural circuits and find, for these nematode worms, that simplicity is the rule,” says George Gilchrist, program director in NSF’s Division of Environmental Biology (in the Directorate for Biological Sciences), which funds BEACON. “By including functional information about each node in the circuit, they have begun decoding the role of natural selection in shaping the architecture of neural circuits.” […] from Danielle J. Whittaker “Understanding the Brain as a Computational Network“, NSF, April 2011.
Drawing (Pedigree of Man, 1879) – Ernst Haeckel‘s “tree of life”, Darwin‘s metaphorical description of the pattern of universal common descent made literal by his greatest popularizer in the German scientific world. This is the English version of Ernst Haeckel‘s tree from the The Evolution of Man (published 1879), one of several depictions of a tree of life by Haeckel. “Man” is at the crown of the tree; for Haeckel, as for many early evolutionists, humans were considered the pinnacle of evolution.
“I was never interested in Facebook or MySpace because they feel like malls to me. Twitter actually feels like the street. You can bump into anybody on Twitter.” — Science-fiction novelist William Gibson – New York (October 11, 2010)
“There is almost certainly an evolutionary drive toward increasing complexity in the face of entropy. That’s practically a definition of life. Technology is so powerful and attractive to us because it holds the promise of greater complexity and greater connectedness. Atoms to molecules to cells to organelles to organisms. What’s next? No one knows for sure, but it sure ain’t Facebook.” — American media theorist Douglas Rushkoff, writer, columnist, early cyberpunk culture adopter, and advocacy of open source solutions to social problems.
Precursors of social networks in the late 1800s include Émile Durkheim and Ferdinand Tönnies. Tönnies argued that social groups can exist as personal and direct social ties that either link individuals who share values and belief (gemeinschaft) or impersonal, formal, and instrumental social links (gesellschaft) [in Linton Freeman, “The Development of Social Network Analysis“, Vancouver, Empirical Press, 2004 (here is a valuable must-read review on it)]. Durkheim gave a non-individualistic explanation of social facts arguing that social phenomena arise when interacting individuals constitute a reality that can no longer be accounted for in terms of the properties of individual actors. He distinguished between a traditional society – “mechanical solidarity” – which prevails if individual differences are minimized, and the modern society – “organic solidarity” – that develops out of cooperation between differentiated individuals with independent roles. Then, Georg Simmel (1908-1971), writing at the turn of the twentieth century, was the first scholar to think directly in social network terms. His essays pointed to the nature of network size on interaction and to the likelihood of interaction in ramified, loosely-knit networks rather than groups.
Nowadays, however, the paraphernalia of increasing intelligent tools (network metrics) are widely available, mainly to the exponential role of the science of complex networks. As stated by Matthias Scholz (Network Science.org / Webpage) (…) Network science has received a major boost caused by the widespread availability of huge network data resources in the last years. One of the most surprising findings, popularized by Albert-László Barabási and his team, is that real networks behave very distinct from traditional assumptions of network theory. Traditionally, real networks were supposed to have a majority of nodes of about the same number of connections around an average. This is typically modelled by random graphs. However, modern network research revealed that the majority of nodes of real networks is very low connected, and, by contrast, there exists some nodes of very extreme connectivity (hubs). This power-law characteristics, termed scale-free by Barabási, can be found in many complex real networks from biological (natural) to social man-made networks (…).
Book cover – Linton Freeman, “The Development of Social Network Analysis“, Vancouver, Empirical Press, 2004 (and a valuable review on it).
While embedding themselves on social-networking, people do tend to forget this, of course, but here are 2 or 3 things you should know about Social Networks before stupefying registering yourself on FarmVille (actually, this is a limited list of some of the actual metrics usually employed on current network analysis provided with a short description – So, … do really ponder yourself where you are – on the street or in the mall!):
Betweenness (link) The extent to which a node lies between other nodes in the network. This measure takes into account the connectivity of the node’s neighbours, giving a higher value for nodes which bridge clusters. The measure reflects the number of people who a person is connecting indirectly through their direct links. | Bridge (link) An edge is said to be a bridge if deleting it would cause its endpoints to lie in different components of a graph. | Centrality (link) This measure gives a rough indication of the social power of a node based on how well they “connect” the network. “Betweenness”, “Closeness”, and “Degree” are all measures of centrality. | Centralization (link) The difference between the number of links for each node divided by maximum possible sum of differences. A centralized network will have many of its links dispersed around one or a few nodes, while a decentralized network is one in which there is little variation between the number of links each node possesses. | Closeness (link) The degree an individual is near all other individuals in a network (directly or indirectly). It reflects the ability to access information through the “grapevine” of network members. Thus, closeness is the inverse of the sum of the shortest distances between each individual and every other person in the network. The shortest path may also be known as the “geodesic distance”. | Clustering coefficient (link) A measure of the likelihood that two associates of a node are associates themselves. A higher clustering coefficient indicates a greater ‘cliquishness’. | Cohesion (link) The degree to which actors are connected directly to each other by cohesive bonds. Groups are identified as ‘cliques’ if every individual is directly tied to every other individual, ‘social circles’ if there is less stringency of direct contact, which is imprecise, or as structurally cohesive blocks if precision is wanted. | …
Fig. – Hue (from red=0 to blue=max) shows the node betweenness. (link)
… Degree (link) The count of the number of ties to other actors in the network. See also degree (graph theory). | (Individual-level) Density (link) The degree a respondent’s ties know one another/ proportion of ties among an individual’s nominees. Network or global-level density is the proportion of ties in a network relative to the total number possible (sparse versus dense networks). | Flow betweenness centrality (link) The degree that a node contributes to sum of maximum flow between all pairs of nodes (not that node). | Eigenvector centrality (link) A measure of the importance of a node in a network. It assigns relative scores to all nodes in the network based on the principle that connections to nodes having a high score contribute more to the score of the node in question. | Local Bridge (link) An edge is a local bridge if its endpoints share no common neighbors. Unlike a bridge, a local bridge is contained in a cycle. | Path Length (link) The distances between pairs of nodes in the network. Average path-length is the average of these distances between all pairs of nodes. | Prestige (link) In a directed graph prestige is the term used to describe a node’s centrality. “Degree Prestige”, “Proximity Prestige”, and “Status Prestige” are all measures of Prestige. See also degree (graph theory). | Radiality (link) Degree an individual’s network reaches out into the network and provides novel information and influence. | Reach (link) The degree any member of a network can reach other members of the network. | Structural cohesion (link) The minimum number of members who, if removed from a group, would disconnect the group. | Structural equivalence (link) Refers to the extent to which nodes have a common set of linkages to other nodes in the system. The nodes don’t need to have any ties to each other to be structurally equivalent. | Structural hole (link) Static holes that can be strategically filled by connecting one or more links to link together other points. Linked to ideas of social capital: if you link to two people who are not linked you can control their communication.
Of course, some of these metrics are redundant over each other, and in fact there is some intelligence on having this on-purpose redundancy. But I would say that Path Length and Cliqueness, Eigenvector centrality, Betweenness, Clustering coefficient, Degree and last but not least Flow (btw, here‘s my own poetic lateral view of it), would be the most important of them all, even if, these all depends on what you are, on what you see, on what you feel, and mostly on what you somehow rather expect from it as a whole experience over time. So, finally, let me just add that all these metrics will not avoid people from writing/sharing experiences like: “Son las 7 y 30 y estoy cagando” followed by “Son las 5 y 31 y ya cagado“. Unfortunately, what follows is precisely a video parody on Facebook not far from his own reality. As usual, you are always free to choose from the geriatric-like shelter malls or the open-air streets…
“How we engage the dance between structure and flow becomes our unique creative signature“, ~ Michelle James, VA, USA, 2010.
[…] Abstract.: The problem of sending the maximum amount of flow q between two arbitrary nodes s and t of complex networks along links with unit capacity is studied, which is equivalent to determining the number of link-disjoint paths between s and t. The average of q over all node pairs with smaller degree kmin is <q>=kmin ~= c.kmin for large kmin with c a constant implying that the statistics of q is related to the degree distribution of the network. The disjoint paths between hub nodes are found to be distributed among the links belonging to the same edge-biconnected component, and q can be estimated by the number of pairs of edge-biconnected links incident to the start and terminal node. The relative size of the giant edge-biconnected component of a network approximates to the coefficient c. The applicability of our results to real world networks is tested for the Internet at the autonomous system level. […], in D.-S. Lee and H. Rieger, “Maximum flow and topological structure of complex networks“, EPL Journal, Europhysics Letters, Vol. 73, Number 3, p.471, 2006. [link] …
“Artificial Life 101” lesson nº1: emerge yourself a experimental “fire” and observe it carefully till the end.
… The other day I decided to work for almost 48 hours in a row and at the end… to sleep a few hours. When I woke up… – the day (e.g. “flow“) was almost gone, and night (e.g. “structure“) approaching fast -. So I decided, to grab the last sun rays… ; growing up, I guess…
Caption – 1st page of Erdös, P.; Rényi, A. (1960). “On The Evolution of Random Graphs“. Magyar Tud. Akad. Mat. Kutató Int. Közl. 5: 17 [PDF].
Documentary film – “N is a Number: A Portrait of Paul Erdös” directed by George Csicsery | 1993 | 57 min. (9 parts)
“There are three signs of senility. The first sign is that a man forgets his theorems. The second sign is that he forgets to zip up. The third sign is that he forgets to zip down“, Paul Erdös.
Paul Erdös was an immensely prolific and notably eccentric Hungarian mathematician. Erdös published more papers than any other mathematician in history, working with hundreds of collaborators. He worked on problems in combinatorics, graph theory, number theory, classical analysis, approximation theory, set theory, and probability theory. He wrote around 1,475 mathematical articles in his lifetime, mostly with co-authors. He strongly believed in and practised mathematics as a social activity, having 511 different collaborators in his lifetime (source).
Having no home, while globe trotting the world from place to place, living mostly for short periods in friend’s and colleagues houses, almost as if he was travelling from one set of mathematics, to another, it was not only the quantity of his work which was tremendous, but mainly the quality and impact of his works. It was not rare, that a single paper, produced a entire brand new field of research. One of my favourite examples, it’s his paper with Rényi on random graphs (image caption above): Erdös, P.; Rényi, A. (1960). “On The Evolution of Random Graphs“. Magyar Tud. Akad. Mat. Kutató Int. Közl. 5: 17 [PDF]. Alone, this single 5 pages paper emerged a new science branch, critical in our times: Complex Networks. The work is now being cited +2500 times.
Fig. – Erdös and Rényi (1959, 1960, 1961) were the first to introduce the concept of random graphs in 1959. The simple model of a network involves taking some number of vertices, N and connecting nodes by selecting edges from the N(N-1)/2 possible edges at random (Albert and Barabási 2002; Newman 2003). Figure shows three random graphs where the probability of an edge being selected is p=0, p=0.1 and p=0.2. (a) Initially 20 nodes are isolated. (b) Pairs of nodes are connected with a probability of p of selecting an edge. In this case (b) p=0.1 , (c) p=0.2, notice how the nodes become quickly connected. The Erdös and Rényi random graph studies explore how the expected topology of the random graph changes as a function of the number of links. It has been shown that when the number of links is below 1/N, the graph is fragmented into small isolated clusters. Above this threshold the network becomes connected as one single cluster or giant component. We now know, that at the threshold the behaviour is indeterminate (Strogatz 2001). Random graphs also show the emergence of subgraphs (below). Erdös and Rényi explored the emergence of these structures, which form patterns such as trees, cycles and loops. Like the giant component, these subgraphs have distinct thresholds where they forming different patterns (below).
Fig. – Different subgraphs appear at varying threshold probabilities in a random graph (Albert and Barabási 2002)
Fig. – Complex Networks (examples): (a) the Internet, where nodes are routers and edges show physical network connections. (b) an ecosystem (c) professional collaboration networks between doctors; and (d) rail network of Barcelona, where nodes are subway stations and edges represent rail connections. (ANU E Press: Australian University Press)
[…] Social networks are either a) going to morph into storytelling media that provide tools to construct narrative on top of the update stream, or b) are going to stop growing as people seek out a different set of tools that are better for communication and storytelling than social networks, which do a mediocre job at both. Part of where I think social networks need to move is to give people the ability to author stories, and to recruit and notify others that they are part of that story. The best online games make this explicit – you participate precisely because you want to be part of a story. Joining a group isn’t a story. Stories have focal points – beginnings and ends. […], Anthony Townsend, “The Future of Social Networks is Storytelling” (part 2), Feb. 2010 [link].
[…] What about writing should be cherished? Calvino, in a wonderfully simple scheme, devotes one lecture (a memo for his reader) to each of five indispensable literary values. First there is “lightness” (leggerezza), and Calvino cites Lucretius, Ovid, Boccaccio, Cavalcanti, Leopardi, and Kundera–among others, as always–to show what he means: the gravity of existence has to be borne lightly if it is to be borne at all. There must be “quickness,” a deftness in combining action (Mercury) with contemplation (Saturn). Next is “exactitude,” precision and clarity of language. The fourth lecture is on “visibility,” the visual imagination as an instrument for knowing the world and oneself. Then there is a tour de force on “multiplicity,” where Calvino brilliantly describes the eccentrics of literature (Elaubert, Gadda, Musil, Perec, himself) and their attempt to convey the painful but exhilarating infinitude of possibilities open to humankind.
The sixth and final lecture – worked out but unwritten – was to be called “Consistency.” Perhaps surprised at first, we are left to ponder how Calvino would have made that statement, and, as always with him, the pondering leads to more. With this book Calvino gives us the most eloquent, least defensive “defense of literature” scripted in our century – a fitting gift for the next millennium. […], Harvard University Press on the Charles Eliot Norton Lectures, (book) Italo Calvino “Six Memos for the next Millenium“. [link]
Chemoton § Vitorino Ramos' research notebook 
Recent Comments