In order to solve hard combinatorial optimization problems (e.g. optimally scheduling students and teachers along a week plan on several different classes and classrooms), one way is to computationally mimic how ants forage the vicinity of their habitats searching for food. On a myriad of endless possibilities to find the optimal route (minimizing the travel distance), ants, collectively emerge the solution by using stigmergic signal traces, or pheromones, which also dynamically change under evaporation.
Current algorithms, however, make only use of a positive feedback type of pheromone along their search, that is, if they collectively visit a good low-distance route (a minimal pseudo-solution to the problem) they tend to reinforce that signal, for their colleagues. Nothing wrong with that, on the contrary, but no one knows however if a lower-distance alternative route is there also, just at the corner. On his global search endeavour, like a snowballing effect, positive feedbacks tend up to give credit to the exploitation of solutions but not on the – also useful – exploration side. The upcoming potential solutions can thus get crystallized, and freeze, while a small change on some parts of the whole route, could on the other-hand successfully increase the global result.
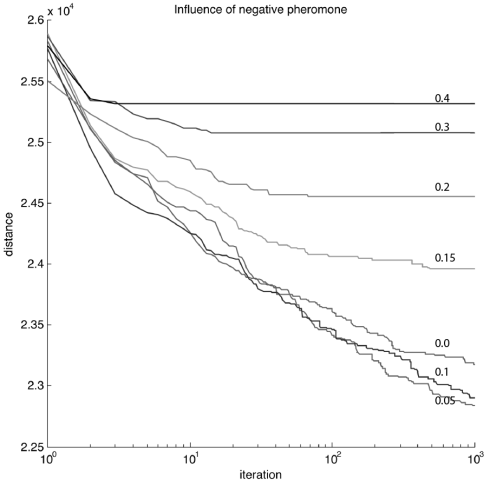 Figure – Influence of negative pheromone on kroA100.tsp problem (fig.1 – page 6) (values on lines represent 1-ALPHA). A typical standard ACS (Ant Colony System) is represented here by the line with value 0.0, while better results could be found by our approach, when using positive feedbacks (0.95) along with negative feedbacks (0.05). Not only we obtain better results, as we found them earlier.
Figure – Influence of negative pheromone on kroA100.tsp problem (fig.1 – page 6) (values on lines represent 1-ALPHA). A typical standard ACS (Ant Colony System) is represented here by the line with value 0.0, while better results could be found by our approach, when using positive feedbacks (0.95) along with negative feedbacks (0.05). Not only we obtain better results, as we found them earlier.
There is, however, an advantage when a second type of pheromone (a negative feedback one) co-evolves with the first type. And we decided to research for his impact. What we found out, is that by using a second type of global feedback, we can indeed increase a faster search while achieving better results. In a way, it’s like using two different types of evaporative traffic lights, in green and red, co-evolving together. And as a conclusion, we should indeed use a negative no-entry signal pheromone. In small amounts (0.05), but use it. Not only this prevents the whole system to freeze on some solutions, to soon, as it enhances a better compromise on the search space of potential routes. The pre-print article is available here at arXiv. Follows the abstract and keywords:
Vitorino Ramos, David M. S. Rodrigues, Jorge Louçã, “Second Order Swarm Intelligence” [PDF], in Hybrid Artificial Intelligent Systems, Lecture Notes in Computer Science, Springer-Verlag, Volume 8073, pp. 411-420, 2013.
Abstract: An artificial Ant Colony System (ACS) algorithm to solve general purpose combinatorial Optimization Problems (COP) that extends previous AC models [21] by the inclusion of a negative pheromone, is here described. Several Travelling Salesman Problem‘s (TSP) were used as benchmark. We show that by using two different sets of pheromones, a second-order co-evolved compromise between positive and negative feedbacks achieves better results than single positive feedback systems. The algorithm was tested against known NP complete combinatorial Optimization Problems, running on symmetrical TSPs. We show that the new algorithm compares favourably against these benchmarks, accordingly to recent biological findings by Robinson [26,27], and Grüter [28] where “No entry” signals and negative feedback allows a colony to quickly reallocate the majority of its foragers to superior food patches. This is the first time an extended ACS algorithm is implemented with these successful characteristics.
Keywords: Self-Organization, Stigmergy, Co-Evolution, Swarm Intelligence, Dynamic Optimization, Foraging, Cooperative Learning, Combinatorial Optimization problems, Symmetrical Travelling Salesman Problems (TSP).

5 comments
Comments feed for this article
7 November, 2013 at 9:19 pm
Second Order Swarm Intelligence | DA6NCI
[…] Artificial Intelligence, Biomimicry, Collective, Complexity, Computation, Swarmadmin ORIGINAL: Chemoton § Vitorino Ramos’ research notebook7 November, […]
7 November, 2013 at 9:32 pm
Second Order Swarm Intelligence | Bounded Ratio...
[…] In order to solve hard combinatorial optimization problems (e.g. optimally scheduling students and teachers along a week plan on several different classes and classrooms), one way is to computationally mimic how ants forage the vicinity of their habitats searching for food. On a myriad of endless possibilities to find the optimal route (minimizing the travel distance), ants, collectively emerge the solution by using stigmergic signal traces, or pheromones. […]
7 November, 2013 at 9:33 pm
Second Order Swarm Intelligence | Knowledge Team
[…] See on chemoton.wordpress.com […]
12 November, 2013 at 10:09 pm
Machine Learning | Pearltrees
[…] Second Order Swarm Intelligence | Chemoton § Vitorino Ramos' research notebook […]
22 November, 2013 at 9:36 am
Second Order Swarm Intelligence | Aural Complex...
[…] In order to solve hard combinatorial optimization problems (e.g. optimally scheduling students and teachers along a week plan on several different classes and classrooms), one way is to computation… […]